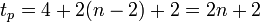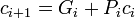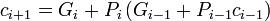Half Adder
Consider adding two binary numbers together:We see that the bit in the "two's" column is generated when the addition carried over. A half-adder is a circuit which adds two bits together and outputs the sum of those two bits. The half-adder has two outputs: sum and carry. Sum represents the remainder of the integer division A+B/2, while carry is the result. This can be expressed as follows:
|
Full Adder
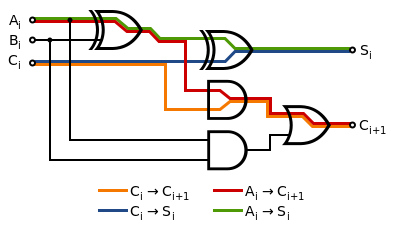
Half-adders have a major limitation in that they cannot accept a carry bit from a previous stage, meaning that they cannot be chained together to add multi-bit numbers. However, the two output bits of a half-adder can also represent the result A+B=3 as sum and carry both being high.As such, the full-adder can accept three bits as an input. Commonly, one bit is referred to as the carry-in bit. Full adders can be cascaded to produce adders of any number of bits by daisy-chaining the carry of one output to the input of the next.
|
Ripple-Carry Adder
A ripple carry adder is simple several full adders connected in a series so that the carry must propagate through every full adder before the addition is complete. Ripple carry adders require the least amount of hardware of all adders, but they are the slowest.The following diagram shows a four-bit adder, which adds the numbers A[3:0] and B[3:0], as well as a carry input, together to produce S[3:0] and the carry output.
Propagation Delay in Full Adders
Real logic gates do not react instantaneously to the inputs, and therefore digital circuits have a maximum speed. Usually, the delay through a digital circuit is measured in gate-delays, as this allows the delay of a design to be calculated for different devices. AND and OR gates have a nominal delay of 1 gate-delay, and XOR gates have a delay of 2, because they are really made up of a combination of ANDs and ORs.A full adder block has the following worst case propagation delays:
- From Ai or Bi to Ci+1: 4 gate-delays (XOR → AND → OR)
- From Ai or Bi to Si: 4 gate-delays (XOR → XOR)
- From Ci to Ci+1: 2 gate-delays (AND → OR)
- From Ci to Si: 2 gate-delays (XOR)
- 4 gate-delays from generating the first carry signal (A0/B0 → C1).
- 2 gate-delays per intermediate stage (Ci → Ci+1).
- 2 gate-delays at the last stage to produce both the sum and carry-out outputs (Cn-1 → Cn and Sn-1).
Carry-Lookahead Adder
A fast method of adding numbers is called carry-lookahead. This method doesn't require the carry signal to propagate stage by stage, causing a bottleneck. Instead it uses additional logic to expedite the propagation and generation of carry information, allowing fast addition at the expense of more hardware requirements.In a ripple adder, each stage compares the carry-in signal, Ci, with the inputs Ai and Bi and generates a carry-out signal Ci+1 accordingly. In a carry-lookahed adder, we define two new function.
The generate function, Gi, indicates whether that stage causes a carry-out signal Ci to be generated if no carry-in signal exists. This occurs if both the addends contain a 1 in that bit:
| Ai | Bi | Ci | Gi | Pi | Ci+1 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
| Operation | Required Data | Gate Delays |
|---|---|---|
| Produce stage generate and propagate signals | Addends (a and b) | 1 |
| Produce stage carry-out signals, C1 to Cn | P and G signals, and C0 | 2 |
| Produce sum result, S | Carry signals and addends | 3 |
| Total | 6 | |
For a slightly smaller circuit, the propagate signal can be taken as the output of the first XOR gate instead of using a dedicated OR gate, because if both A and B are asserted, the generate signal will force a carry. However, this simplifiaction means that the propagate signal will take two gate delays to produce, rather than just one.
A carry lookahead adder then contains n PFAs and the logic to produce carries from the stage propagate and generate signals:
Two numbers can therefore be added in constant time, O(1), of just 6 gate delays, regardless of the length, n of the numbers. However, this requires AND and OR gates with up to n inputs. If logic gates are available with a limited number of inputs, trees will need to be constructed to compute these, and the overall computation time is logarithmic, O(ln(n)), which is still much better than the linear time for ripple adders.
Cascading Carry-Lookahead Adders
A basic carry-lookahead adder is very fast but has the disadvantage that it takes a very large amount of logic hardware to implement. In fact, the amount of hardware needed is approximately quadratic with n, and begins to get very complicated for n greater than 4.Due to this, most CLAs are constructed out of "blocks" comprising 4-bit CLAs, which are in turn cascaded to produce a larger CLA.
Carry-Save Adder
This section of the Digital Circuits wikibook is a stub. You can help by expanding this section. If you add something, list yourself as a Contributor.A carry-save adder is a kind of adder with low propagation delay (critical path), but instead of adding two input numbers to a single sum output, it adds three input numbers to an output pair of numbers. When its two outputs are then summed by a traditional carry-lookahead or ripple-carry adder, we get the sum of all three inputs.
When adding three or more numbers together, a sequence of carry-save adders terminated by a single carry-lookahead adder provides much better propagation delays than a sequence of carry-lookahead adders. In particular, the propagation delay of a carry-save adder is not affected by the width of the vectors being added.
Carry-save adders are really completely parallel arrays of full adder circuits, with the each bit of the three input vectors loaded into each full adder's A, B, and Cin inputs. Each full adder's output S is connected to the corresponding output bit of one output, and its output Cout is connected to the next higher output bit of the second output; the lowest bit of the second output is fed directly from the carry-save's Cin input.