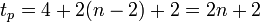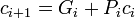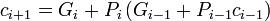Joomla Vs Wordpress

Read more...

ΕΑΠ: Μάθετε τι πιθανότητες έχετε να κληρωθεί το όνομα σας (πηγη: News.gr - Καλόγηρος Βασίλειος)

Τις 40.000 περίπου έφθασαν οι αιτήσεις στο Ανοικτό Πανεπιστήμιο για τα προπτυχιακά και μεταπτυχιακό προγράμματα σπουδών. Το ενδιαφέρον των υποψηφίων ήταν αυξημένο, παρά την οικονομική κρίση και το γεγονός ότι οι σπουδές στο ΕΑΠ απαιτούν την καταβολή διδάκτρων.

Όπως έχουμε γράψει τα δίδακτρα για τα προπτυχιακά προγράμματα διαμορφώνονται στα 6.600 ευρώ και στα μεταπτυχιακά στα 3.500 ευρώ.

Το news παρουσιάζει στους ακόλουθες πίνακες τις πιθανότητες επιλογής με βάση τον αριθμό των αιτήσεων και τις προσφερόμενες θέσεις. Σε προγράμματα που παραδοσιακά υπάρχει μεγάλη ζήτηση όπως το μεταπτυχιακό «Σπουδές στην Εκπαίδευση» οι πιθανότητες διαμορφώνονται περίπου στο 11% ενώ και στο μεταπτυχιακό «Master in Business Administration» όπου υποβλήθηκαν 1.943 αιτήσεις οι πιθανότητες ανέρχονται στις 13.38 ποσοστιαίες μονάδες.

Αρκετή τύχη χρειάζονται και όσοι έχουν επιλέξει το μεταπτυχιακό στην «Εκπαίδευση Ενηλίκων Γ (χωρίς Θ.Ε)» αφού και εκεί οι πιθανότητες είναι 9.28%. Αντίθετα, όπως έγραψε το news.gr,  υπάρχουν προγράμματα που λόγω των προϋποθέσεων δέχτηκαν μικρό αριθμό αιτήσεων και οι υποψήφιοι γνωρίζουν από τώρα ότι είναι φοιτητές.

Στα προπτυχιακά προγράμματα και ειδικά στη «Διοίκηση Επιχειρήσεων» αναμένεται να χαμογελάσει  1 στους 5 υποψηφίους αφού οι πιθανότητες διαμορφώνονται στο 23.5%.  Τις πιθανότητες με το μέρος τους έχουν όσοι επέλεξαν το πρόγραμμα «Σπουδές στον Ευρωπαϊκό Πολιτισμό» καθώς με βάση τις αιτήσεις 1 στους 2 θα επιλεχθεί.

Αξίζει να σημειωθεί ότι η κλήρωση θα πραγματοποιηθεί στις 15 Δεκεμβρίου ενώ θα αναρτηθούν στην ιστοσελίδα του ΕΑΠ, μετά την ολοκλήρωση της διαδικασίας οι πίνακες Α όπου εντάσσονται όσοι επιλέχθηκαν, ο πίνακας Β όπου εντάσσονται οι επιλαχόντες που καλούνται και αυτοί να καταθέσουν  τα δικαιολογητικά τους χωρίς όμως να αποστείλουν χρήματα.

Τέλος υπάρχει και  ο πίνακας Γ όπου όσοι είναι σε αυτόν έχουν περιορισμένες πιθανότητες. Οι ανήκοντες στην κατηγορία αυτή έχουν πιθανότητα εγγραφής υπό την προϋπόθεση ότι θα παραμείνουν κενές θέσεις από τις κατηγορίες Α και Β, τόσες που να φθάνουν τον αύξοντα αριθμό κατάταξης κάποιου από την κατηγορία Γ.

Μεταπτυχιακό πρόγραμμα	Θέσεις	Αιτήσεις	Πιθανότητες
Τεχνολογία Υλικού και Λογισµικού Β (Προγ.2)	9	2	450,00%
Περιβαλλοντικός Σχεδιασµός Πόλεων και Κτιρίων Γ (Πρ.3)	29	22	131,82%
Περιβαλλοντικός Σχεδιασµός Πόλεων και Κτιρίων Γ (Πρ.3) 10 ΕΤΗ	6	6	100,00%
Μεταπτυχιακή Εξειδίκευση Καθηγητών Γαλλικής	70	74	94,59%
Σεισµική Μηχανική και Αντισεισµικές Κατασκευές Α (Πρ.1)	70	78	89,74%
Μεταπτυχιακή Εξειδίκευση Καθηγητών Γερµανικής	45	55	81,82%
Περιβαλλοντικός Σχεδιασµός Πόλεων και Κτιρίων Α (Πρ.1) 10 ΕΤΗ	15	21	71,43%
Προχωρηµένες Σπουδές στη Φυσική	30	48	62,50%
Περιβαλλοντικός Σχεδιασµός Πόλεων και Κτιρίων Α (Πρ.1)	55	90	61,11%
Περιβαλλοντικός Σχεδιασµός Έργων Υποδοµής Α&Β (Πρ.1)	88	145	60,69%
∆ιοίκηση Τουριστικών Επιχειρήσεων (10ΕΤΗ)	80	160	50,00%
Διαχείριση Τεχνικών Έργων Α (Προγ.1)	206	424	48,58%
Περιβαλλοντικός Σχεδιασµός Έργων Υποδοµής Α&Β (Πρ.1) 10 ΕΤΗ	20	43	46,51%
Μεταπτυχιακή Εξειδίκευση Καθηγητών των Φυσικών Επιστημών	60	135	44,44%
Σχεδιασµός Φωτισµού Πολυµέσα Α (Προγ. 1)	42	97	43,30%
Περιβαλλοντικός Σχεδιασµός Πόλεων και Κτιρίων Β (Πρ.2)	34	81	41,98%
Μεταπτυχιακές Σπουδές στα Μαθηµατικά	90	234	38,46%
Κατάλυση και Προστασία του Περιβάλλοντος	45	124	36,29%
Διαχείριση Αποβλήτων (10ΕΤΗ)	55	152	36,18%
Τεχνολογία Υλικού και Λογισµικού Α (Προγ. 1)	81	234	34,62%
Διασφάλιση Ποιότητας (10 ΕΤΗ)	75	217	34,56%
Μεταπτυχιακή Εξειδίκευση Καθηγητών Αγγλικής	120	392	30,61%
Διαχείριση Τεχνικών Έργων Α (Προγ.1) (10 ΕΤΗ)	50	170	29,41%
Σπουδές στην Ορθόδοξη Θεολογία Α (Προγ. 1)	36	124	29,03%
Διασφάλιση Ποιότητας	295	1019	28,95%
Ακουστικός Σχεδιασμός και Πολυμέσα	30	109	27,52%
Διαχείριση Αποβλήτων	225	862	26,10%
∆ιοίκηση Τουριστικών Επιχειρήσεων	310	1225	25,31%
Περιβαλλοντικός Σχεδιασµός Πόλεων και Κτιρίων Β (Πρ.2) 10 ΕΤΗ	8	32	25,00%
Σεισµική Μηχανική και Αντισεισµικές Κατασκευές Β (Πρ.2)	15	60	25,00%
∆ιοίκηση Πολιτισµικών Μονάδων (10ΕΤΗ)	80	336	23,81%
Γραφικές Τέχνες - Πολυμέσα	60	254	23,62%
Τραπεζική (10ΕΤΗ)	100	439	22,78%
Μεταπτυχιακή Εξειδίκευση στα Πληροφοριακά Συστήματα	100	502	19,92%
∆ιοίκηση Επιχειρήσεων (ΜΒΑ) (10ΕΤΗ)	90	452	19,91%
Σπουδές στην Ορθόδοξη Θεολογία Β (Προγ. 2)	54	277	19,49%
Τραπεζική	355	1862	19,07%
∆ιοίκηση Μονάδων Υγείας	315	1661	18,96%
∆ιοίκηση Πολιτισµικών Μονάδων	320	1872	17,09%
Περιβαλλοντικός Σχεδιασµός Έργων Υποδοµής Γ (Πρ.2) 10 ΕΤΗ	2	12	16,67%
∆ιοίκηση Μονάδων Υγείας (10ΕΤΗ)	80	548	14,60%
Σχεδιασµός Φωτισµού Πολυµέσα Β (Προγ. 2)	18	124	14,52%
Κοινό ΜΠΣ Master in Business Administration	260	1943	13,38%
Εκπαίδευση Ενηλίκων Β (χωρίς Θ.Ε.)	100	771	12,97%
Διαχείριση Τεχνικών Έργων  Β (Προγ.2) (10 ΕΤΗ)	14	110	12,73%
Σπουδές στην Εκπαίδευση Με Θεµατικές Ενότητες	10	82	12,20%
Σπουδές στην Εκπαίδευση Β & Γ (χωρίς Θ.Ε.)	540	4631	11,66%
Σπουδές στην Εκπαίδευση Β & Γ (χωρίς Θ.Ε.) (10 ΕΤΗ)	150	1360	11,03%
Περιβαλλοντικός Σχεδιασµός Έργων Υποδοµής Γ (Πρ.2)	10	92	10,87%
Εκπαίδευση Ενηλίκων Γ (χωρίς Θ.Ε.)	110	1185	9,28%
Διαχείριση Τεχνικών Έργων  Β (Προγ.2)	50	601	8,32%
Εκπαίδευση Ενηλίκων Με Θεµατικές  Ενότητες	5	69	7,25%

Προπτυχιακά	Θέσεις	Αιτήσεις	Πιθανότητες
Σπουδές στον Ευρωπαϊκό Πολιτισµό (10ΕΤΗ)	200	309	64,72%
Σπουδές στον Ευρωπαϊκό Πολιτισµό	800	1340	59,70%
Σπουδές στον Ελληνικό Πολιτισµό (10ΕΤΗ)	220	417	52,76%
Σπουδές στις Φυσικές Επιστήµες	200	418	47,85%
Πληροφορική	900	2228	40,39%
Ισπανική Γλώσσα και Πολιτισµός	90	225	40,00%
Σπουδές στον Ελληνικό Πολιτισµό	800	2294	34,87%
∆ιοίκηση Επιχειρήσεων και Οργανισµών	1200	5107	23,50%
∆ιοίκηση Επιχειρήσεων και Οργανισµών (10ΕΤΗ)	300	1626	18,45%

Καλόγηρος Βασίλειος

Read more...

Operating Systems for Toasters.

Read more...

decoder 2 to 4

What are Decoders, and how can we use them ?

Decoders are simply a collection of logic gates which are arranged in a specific way so as to breakdown any combination of inputs to a set of terms that are all set to '0' apart from one term. Therefore when one input changes, two output terms will change. Note that these terms are "minterms", remembering that minterms use a variable once, and once only.
Lets say we have N inputs to a decoder, the number of outputs will be equal to 2^N. Thus there will be one line at the output for each possible input.

Example: Decoder_1

In this example we will learn how a basic decoder works. A two to four line decoder is of the form, two inputs and four outputs. The Flash animation below shows how the inputs are decoded at each stage.
Use the controls to stop the animation at any time.

This diagram shows how a two to four line decoder works with a logic '1,0' on the input.

So now we have the base logic diagram to show how a decoder makes use of simple logic to produce min terms of its input variables.
To express a decoder on a schematic diagram is similar to the diagram for a multiplexor, just the opposite way round.

The truth table for the considered example can be shown as follows.

A	B	Y0	Y1	Y2	Y3
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

Due to the way many logic IC's are made, it is ofter cheaper to purchase inverted decoders. These decoders use NAND gates instead of the AND gates we have seen in the decoder_1 example. In these cases the output to an inverted 2-4 line decoder would be like this:

A	B	Y0	Y1	Y2	Y3
0	0	0	1	1	1
0	1	1	0	1	1
1	0	1	1	0	1
1	1	1	1	1	0

We will cover circuit implementation of both of these types of decoders in the next section of this chapter.
It is worthy to note that decoders that are commonly available are 2-4 line, 3-8 line, and 4-10 line decoders. This has probably been made clear in your course notes.

Before moving on to the next part of this chapter. Make sure you understand how decoders can be made from basic logic gates. (At least using AND gates and NOT gates). To test yourself, you may want to quickly draw the schematic diagram for a 3-8 line decoder, and the truth table. Then start thinking about how decoders can be used to implement functions.

Read more...

Half Adders, Full Adders, Ripple Carry Adders (WIKI BOOKS)

Half Adder

Consider adding two binary numbers together:

We see that the bit in the "two's" column is generated when the addition carried over. A half-adder is a circuit which adds two bits together and outputs the sum of those two bits. The half-adder has two outputs: sum and carry. Sum represents the remainder of the integer division A+B/2, while carry is the result. This can be expressed as follows:

• 
• 

A B A+B S C 0 0 0 0 0 0 1 1 1 0 1 0 1 1 0 1 1 2 0 1

Full Adder

Half-adders have a major limitation in that they cannot accept a carry bit from a previous stage, meaning that they cannot be chained together to add multi-bit numbers. However, the two output bits of a half-adder can also represent the result A+B=3 as sum and carry both being high.
As such, the full-adder can accept three bits as an input. Commonly, one bit is referred to as the carry-in bit. Full adders can be cascaded to produce adders of any number of bits by daisy-chaining the carry of one output to the input of the next.

A B Cin A+B+Cin S Cout 0 0 0 0 0 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 2 0 1 1 0 0 1 1 0 1 0 1 2 0 1 1 1 0 2 0 1 1 1 1 3 1 1

The full-adder is usually shown as a single unit. The sum output is usually on the bottom on the block, and the carry-out output is on the left, so the devices can be chained together, most significant bit leftmost:

Ripple-Carry Adder

A ripple carry adder is simple several full adders connected in a series so that the carry must propagate through every full adder before the addition is complete. Ripple carry adders require the least amount of hardware of all adders, but they are the slowest.
The following diagram shows a four-bit adder, which adds the numbers A[3:0] and B[3:0], as well as a carry input, together to produce S[3:0] and the carry output.

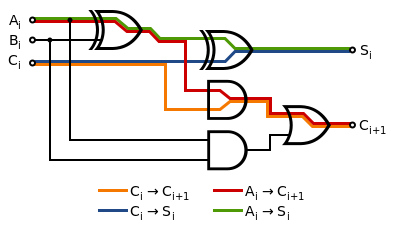
Propagation Delay in Full Adders

Real logic gates do not react instantaneously to the inputs, and therefore digital circuits have a maximum speed. Usually, the delay through a digital circuit is measured in gate-delays, as this allows the delay of a design to be calculated for different devices. AND and OR gates have a nominal delay of 1 gate-delay, and XOR gates have a delay of 2, because they are really made up of a combination of ANDs and ORs.
A full adder block has the following worst case propagation delays:

• From A_i or B_i to C_i+1: 4 gate-delays (XOR → AND → OR)
• From A_i or B_i to S_i: 4 gate-delays (XOR → XOR)
• From C_i to C_i+1: 2 gate-delays (AND → OR)
• From C_i to S_i: 2 gate-delays (XOR)

Because the carry-out of one stage is the next's input, the worst case propagation delay is then:

• 4 gate-delays from generating the first carry signal (A₀/B₀ → C₁).
• 2 gate-delays per intermediate stage (C_i → C_i+1).
• 2 gate-delays at the last stage to produce both the sum and carry-out outputs (C_n-1 → C_n and S_n-1).

So for an n-bit adder, we have a total propagation delay, t_p of:

This is linear in n, and for a 32-bit number, would take 65 cycles to complete the calculation. This is rather slow, and restricts the word length in our device somewhat. We would like to find ways to speed it up.

Carry-Lookahead Adder

A fast method of adding numbers is called carry-lookahead. This method doesn't require the carry signal to propagate stage by stage, causing a bottleneck. Instead it uses additional logic to expedite the propagation and generation of carry information, allowing fast addition at the expense of more hardware requirements.
In a ripple adder, each stage compares the carry-in signal, C_i, with the inputs A_i and B_i and generates a carry-out signal C_i+1 accordingly. In a carry-lookahed adder, we define two new function.
The generate function, G_i, indicates whether that stage causes a carry-out signal C_i to be generated if no carry-in signal exists. This occurs if both the addends contain a 1 in that bit:

The propagate function, P_i, indicates whether a carry-in to the stage is passed to the carry-out for the stage. This occurs if either the addends have a 1 in that bit:

Note that both these values can be calculated from the inputs in a constant time of a single gate delay. Now, the carry-out from a stage occurs if that stage generates a carry (G_i = 1) or there is a carry-in and the stage propagates the carry (P_i·C_i = 1):

The table below summaries this:

Ai	Bi	Ci		Gi	Pi	Ci+1
0	0	0		0	0	0
0	0	1		0	0	0
0	1	0		0	1	0
0	1	1		0	1	1
1	0	0		0	1	0
1	0	1		0	1	1
1	1	0		1	1	1
1	1	1		1	1	1

We can extend the expression for the carry-out by substituting the expression for the carry-out of the previous stage:

Note that this does not require the carry-out signals from the previous stages, so we don't have to wait for changes to ripple through the circuit. In fact, a given stage's carry signal can be computed once the propagate and generate signals are ready with only two more gate delays (one AND and one OR). Thus the carry-out for a given stage can be calculated in constant time, and therefore so can the sum.

Operation	Required Data	Gate Delays
Produce stage generate and propagate signals	Addends (a and b)	1
Produce stage carry-out signals, C1 to Cn	P and G signals, and C0	2
Produce sum result, S	Carry signals and addends	3
Total		6

The S, P, and G signals are all generated by a circuit called a "partial full adder" (PFA), which is similar to a full adder.

For a slightly smaller circuit, the propagate signal can be taken as the output of the first XOR gate instead of using a dedicated OR gate, because if both A and B are asserted, the generate signal will force a carry. However, this simplifiaction means that the propagate signal will take two gate delays to produce, rather than just one.
A carry lookahead adder then contains n PFAs and the logic to produce carries from the stage propagate and generate signals:

Two numbers can therefore be added in constant time, O(1), of just 6 gate delays, regardless of the length, n of the numbers. However, this requires AND and OR gates with up to n inputs. If logic gates are available with a limited number of inputs, trees will need to be constructed to compute these, and the overall computation time is logarithmic, O(ln(n)), which is still much better than the linear time for ripple adders.

Cascading Carry-Lookahead Adders

A basic carry-lookahead adder is very fast but has the disadvantage that it takes a very large amount of logic hardware to implement. In fact, the amount of hardware needed is approximately quadratic with n, and begins to get very complicated for n greater than 4.
Due to this, most CLAs are constructed out of "blocks" comprising 4-bit CLAs, which are in turn cascaded to produce a larger CLA.

Carry-Save Adder

This section of the Digital Circuits wikibook is a stub. You can help by expanding this section. If you add something, list yourself as a Contributor.

A carry-save adder is a kind of adder with low propagation delay (critical path), but instead of adding two input numbers to a single sum output, it adds three input numbers to an output pair of numbers. When its two outputs are then summed by a traditional carry-lookahead or ripple-carry adder, we get the sum of all three inputs.
When adding three or more numbers together, a sequence of carry-save adders terminated by a single carry-lookahead adder provides much better propagation delays than a sequence of carry-lookahead adders. In particular, the propagation delay of a carry-save adder is not affected by the width of the vectors being added.
Carry-save adders are really completely parallel arrays of full adder circuits, with the each bit of the three input vectors loaded into each full adder's A, B, and Cin inputs. Each full adder's output S is connected to the corresponding output bit of one output, and its output Cout is connected to the next higher output bit of the second output; the lowest bit of the second output is fed directly from the carry-save's Cin input.

Read more...